Fibonacci a technikai elemzésben: önmagát beteljesítő jóslat?
Publikációját Liber Abaci, azaz a Számsorozat Könyve címmel jelentette meg, s benne nem csak elméleti gondolatait vázolta fel, hanem számelméletének számos gyakorlati alkalmazhatóságát is bemutatta. A számsorozat első tőzsde alkalmazásáról azonban nem áll rendelkezésre túl sok információ.
A számsorozat képzése
A szorozat képzése nem túl bonyolult, ám annál érdekesebb. A számok meghatározása úgy történik, hogy az első tagot 1-nek vesszük, majd ezt követően a sorozat következő tagját az azt megelőző két szám összegeként kapjuk. Tehát a sorozat tagjai a következők lesznek:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, stb.
Mindazonáltal a Fibonacci számok több érdekességet mutatnak. Ha ugyanis elosztjuk a számokat a sorozat következő elemével, akkor a hányados egy konstans szám, 0.618 felé konvergál, ha a nagyobbal osztjuk el a kisebbet, akkor pedig a hányados 1.1618 felé konvergál. (A két szám a technikai elemzésben használt Fibonacci szintek tárgyalásakor még visszaköszön.)
Ez a szám ismerős lehet sokak számára, hiszen ezt az arányt már az ókori görögök is ismerték, és aranymetszésnek, korábban pedig "isteni aránynak" hívták. Az aranymetszés arányai megdöbbentő módon a természetben és az emberi alkotásokban számtalan helyen megtalálhatóak (virágok alakjai, az A/4-es papírlap oldalainak aránya, növények levelei, pálmafák ágai, a csigavonal arányai, athéni Parthenón, New York.-i ENSZ Palota, kártyák alakjai, az emberi test köldök feletti és alatti része, egyesek szerint a női mellek elhelyezkedése a felsőtesten, stb.).
Az aranymetszés aránya akkor áll fenn, ha a két szakasz közötti arány pontosan megegyezik az egyenes és a nagyobbik szakasz arányával. A két szakasz arányát a matematikában f-vel jelölik.
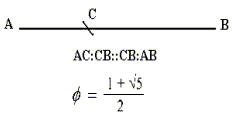
Ha a hitelminősítőnek igaza van, akkor annak durva következménye lesz Magyarországon
A kilátásrontás és ami abból következik.
Ilyen intézkedésekkel tudna a kormány a nyugdíjasok kedvében járni
Farkas András három konkrét kérdéskört vázolt fel.
Az USA feldarabolná Ukrajnát, új offenzívára készül Putyin, – háborús híreink szombaton
A legfontosabb eseményekről folyamatosan beszámolunk.
Súlyos fagy pusztított Törökországban – Egyes régiókban -15 Celsius-fok alá süllyedt a hőmérséklet
Veszélyben az élelmiszerellátás és az inflációs célok.
Milliomosmágnesek: ezek a világ leggazdagabb városai
Mutatunk három érdekes ábrát.
A WTO vezető közgazdásza szerint a vámoktól várt előnyök aligha valósulnak meg
A vámtarifák előnyösek lehetnek azoknak a hazai iparágaknak, amelyek versenyeznek az importált termékekkel.
Top 10 osztalék részvény - 2025. április
Április elsején kijött Justin Law listája az osztalékfizető részvényekről, a Google pedig megtréfált, és berakta az értesítő levelet a spam mappába, ezért csak most csináltam meg a listá
Új lakáshitel konstrukció: akár havi 22 500 Ft kedvezmény a családoknak
HitelesAndrás - Keress, kövess, költözz! Új lakáshitel konstrukció: akár havi 22 500 Ft kedvezmény a családoknak Áprilistól több millió forint maradhat a kasszában Április elsejétől új
Fából készült felhőkarcolók jelenthetik az építészet jövőjét
A modern építészetről a legtöbbeknek a beton, az acél vagy a tégla juthat eszébe alapanyagként, valójában azonban a fa is tökéletesen megfelel erre a célra. Számos vo
Geotermikus energia: a második Trump-ciklus nagy nyertese?
Donald Trump energiaügyi reformjaninak az olajvállalatok mellett a geotermikus energiával foglalkozó cégek lehetnek a legnagyobb nyertesei.
Mit keres Deadpool egy kisvárosban? Hollywoodi sztori Ryan Reynoldsszal
Aki ismeri a walesi csoda alaptörténetét, annak a válasz már részint ismerős lehet. Azonban számos részlet bújik meg a Wrexham AFC hihetetlen felemelkedése mögött. És...
The post Mit keres De![]()
NAV késedelmi pótlék változások 2025-től - havonta kell megfizetni a pótlékot
A NAV 2025-től új rendszert vezet be a késedelmi pótlék kiszabására: az éves egyszeri előírás helyett havi rendszerességgel kerülnek előírásra a késedelmi pótlékok az adószámlán. Ez a![]()
Meg lehet úszni befektetés nélkül? Esnek a piacok!
Mielőtt belekezdünk, előrebocsátom, hogy nem, nem kell kivenned a pénzed a befektetéseidből. Hacsak nem vagy aktív kereskedő, akkor még az éppen aktuális amerikai (vagy kínai/orosz) elnök agy
Itt a 4,75%-os kamatú lakáshitel
Hitelügyintézős Gáborunk írt egy új cikket, a CIB 4,75%-os lakáshiteléről. Ez nem olyan kamu, mint a fiatalok 5%-os lakáshitele, ehhez tényleg hozzá lehet jutni, igaz, CSOK hitelt is kell vele

- Formálódik Donald Trump nagy terve – Ravasz húzással kényszerítené térdre Oroszországot
- Von der Leyen ultimátuma Trumpnak: esélyt ad az EU a tárgyalásoknak, de nem örökké
- Trump meghátrál! Tépik a piacokat
- Itt a Telekom bejelentése: változik az inflációkövető díjkorrekció
- Bod Péter Ákos: Az egész világ megfizeti Trump tévedését


Trump miatt rángatóznak a tőzsdék – Mi jelent most menedéket?
Gyorsan változnak az események Amerikában.
Kockázat vagy lehetőség a génmódosított élelmiszer?
A génmódosítás és a génszerkesztés fontos lehet az élelmezési válság és a klímaváltozás elleni küzdelemben, de sokan félnek tőle.
Nagy hibát vétett Donald Trump, és hol lehet még a szakadék vége?
Folytatódik a vámháború.
Ügyvédek
A legjobb ügyvédek egy helyen
Hogyan vágj bele a tőzsdei befektetésbe?
Első lépések a tőzsdei befektetés terén. Mire kell figyelned? Melyek az első lépések? Mely tőzsdei termékeket célszerű mindenképpen ismerned?
Miért a tőzsdei befektetést válasszam az állampapír helyett?
Online előadásunkon megvizsgáljuk a két befektetési formát, megtárgyaljuk az előnyeiket és a hátrányaikat, sorra vesszük mikor mibe érdemes fektetni.

















