Üzlet
Technikai elemzés: a mozgóátlag használata
De mit is jelent a mozgóátlagolás?.
A statisztikai értelmezés szerint a mozgóátlagolású trendszámítás lényege, hogy az idősor t-edik eleméhez úgy rendelünk hozzá trendértéket, hogy átlagoljuk az idősor t-edik elemének bizonyos környezetében lévő elemeket. Ahogyan tehát a megválasztott periódus halad előre, a legrégebbi adatok mindig kiesnek a mozgóátlagból, és helyükre a legfrissebb adat kerül. Ha tehát a trend számításánál a t-edik elem előtt és után álló elemet vonjuk be a trendbe, azaz a környezetet 1-nek választjuk, akkor a mozgóátlag számítása a következő módon történik:
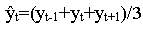
Ebből pedig már egyértelműen következik, hogy a mozgó átlagoknak van egy igen lényeges tulajdonsága, mégpedig az, hogy nem lehet minden egyes elemhez mozgóátlagot számítani, így a megfigyelt idősor eleje és vége elvész.
Ez a formula a legegyszerűbb mozgóátlagolású trendet határozza meg, mely a lehető legegyszerűbben simítja ki az idősort, a t mozgatásával pedig biztosítjuk azt, hogy az alaptendencia megmaradjon. Minél jobban növeljük az átlag számításánál a tagok nagyságát, annál rövidebb lesz a kapott trend, és így természetesen a tendencia felismerése is nehezebb lesz.
A tőzsdei gyakorlatban azonban a mozgóátlagokat nem úgy számítják, hogy a kiválasztott adat környezetében végzik az átlagolást, hanem a kiválasztott adat előtti adatokra, így nem veszik el annyi darab mozgóátlagunk, mint a választott periódus fele. Az átlag számítása tehát nem centrikus, hanem visszatekintő.
A mozgóátlag tehát ebben az esetben is folyamatosan változik az árak változásának hatására, de mindig először az adott részvény, vagy index értéke változik, s csak ezt követően módosul a mozgóátlag értéke, így a mozgóátlag mindig utólag "mond valamit".
